VolgaCTF 2017 Writeup: Transformer
Reversing an encrypter and discovering a whole new mode of encryptionVolgaCTF qualifiers were held last weekend, and this time around I sat in on 0xBU’s team. I managed to solve Transformer, a 400 point reverse engineering challenge, and so here is the requisite writeup.
Decompiler, You Say?
Transformer
We’ve got a file that was processed with a binary called transformer. We really need the contents of this file. Can you help?
ciphertext.zip.enc
transformer
The setup looks pretty straightforward: reverse engineer how transformer has
encrypted ciphertext.zip.enc so we can decrypt it and recover a flag contained
within the zip file. Unfortunately (or not, depending on your point of view) we
are presented with a surprise when loading up the binary into our disassembler.
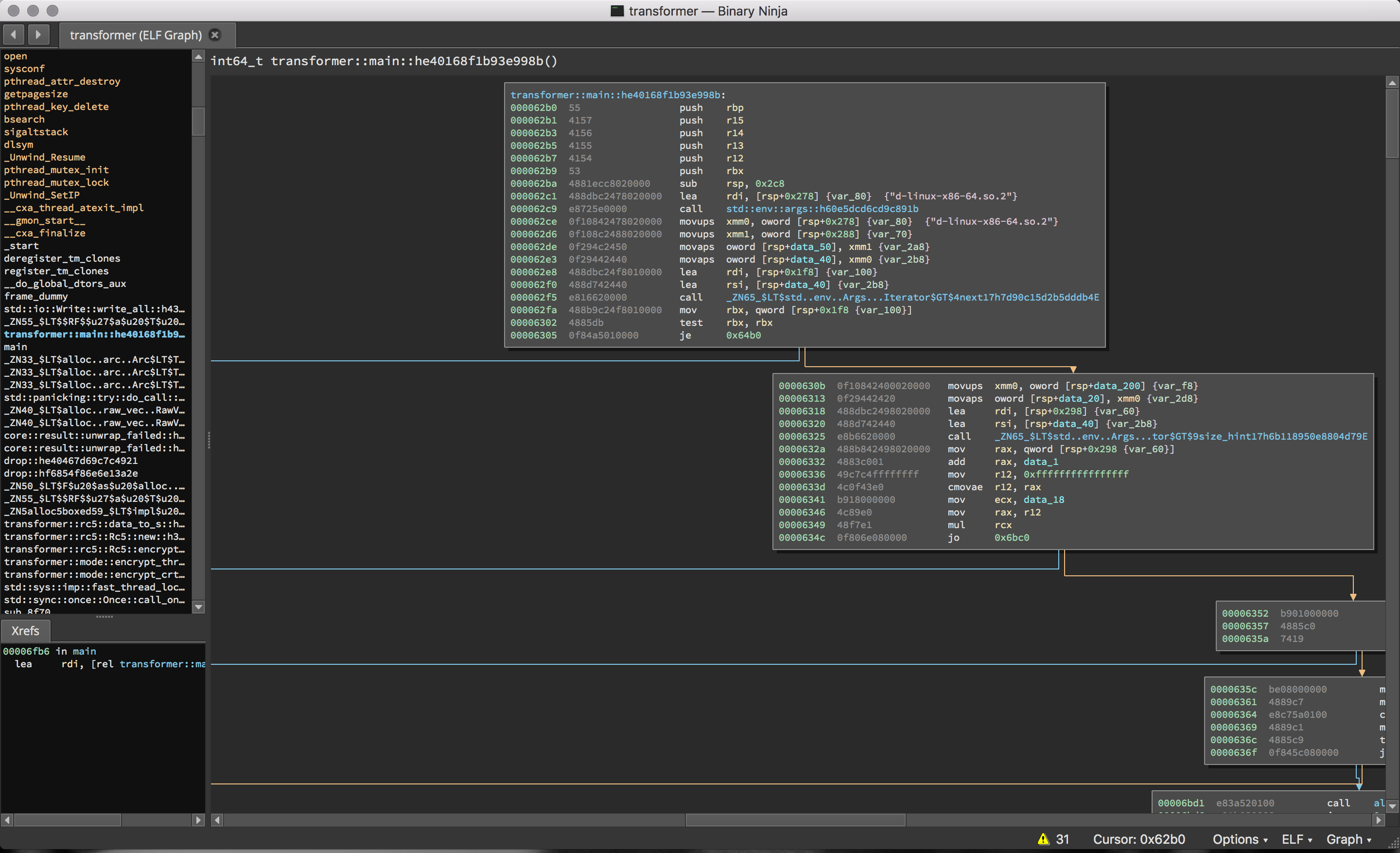
Yes, that’s Rust – currently my favorite language, though I hadn’t ever had to analyze programs authored in it before this CTF. In fact, two of the challenges that I looked at were written in rust, which I assume was done to hinder the use of freely available decompilers like Snowman. If so, nice trick; even at the disassembly level function boundary recognition seems difficult for Binary Ninja.
That being said, one is still able to recognize what’s going on (thankfully, we’re not dealing with a stripped binary). And, it’s not long before it’s clear that we’re looking at RC5 in some configuration. (Of course, this could have been misdirection, but thankfully – again – was not.)
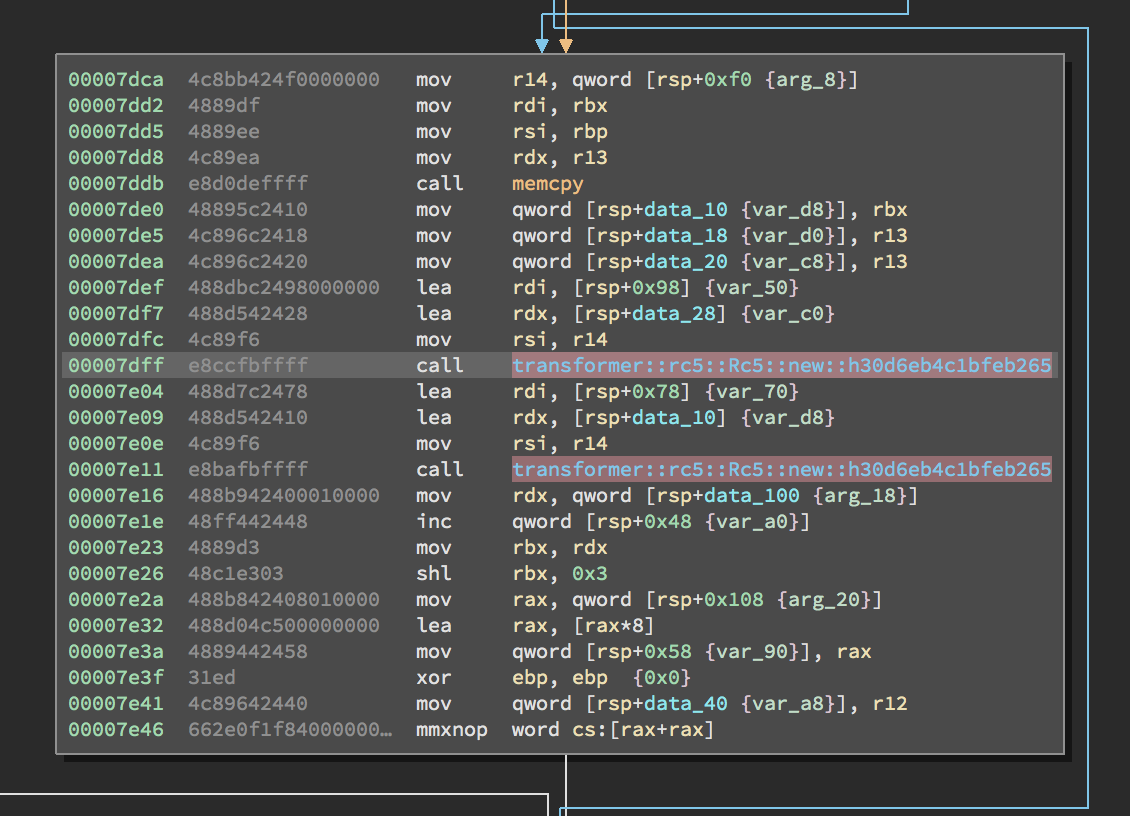
We have two RC5 instances being constructed here, so the first order of business is to figure out how they are being initialized and used.
A “Novel” RC5 Construction
First of all, we clearly want to know how these RC5 instances are being
initialized: where the keys are coming from, what the blocksize is, how many
rounds are being performed, and what mode is used. The keys can be directly
traced to a couple of static arrays which spells good news for our efforts, and
similarly for the number of rounds and blocksize. The name of one of the
functions (transformer::mode::encrypt_crt_ecb) narrows down the encryption
mode, but doesn’t fully answer that question.

<figcaption>Our RC5 keys, statically embedded into the binary as two 8-byte arrays.</figcaption>
Next, we need to see where these RC5 instances are used to perform encryption, on what data, and how (if at all) the output is combined. Luckily, all of these questions are answered not too far away from instance construction.
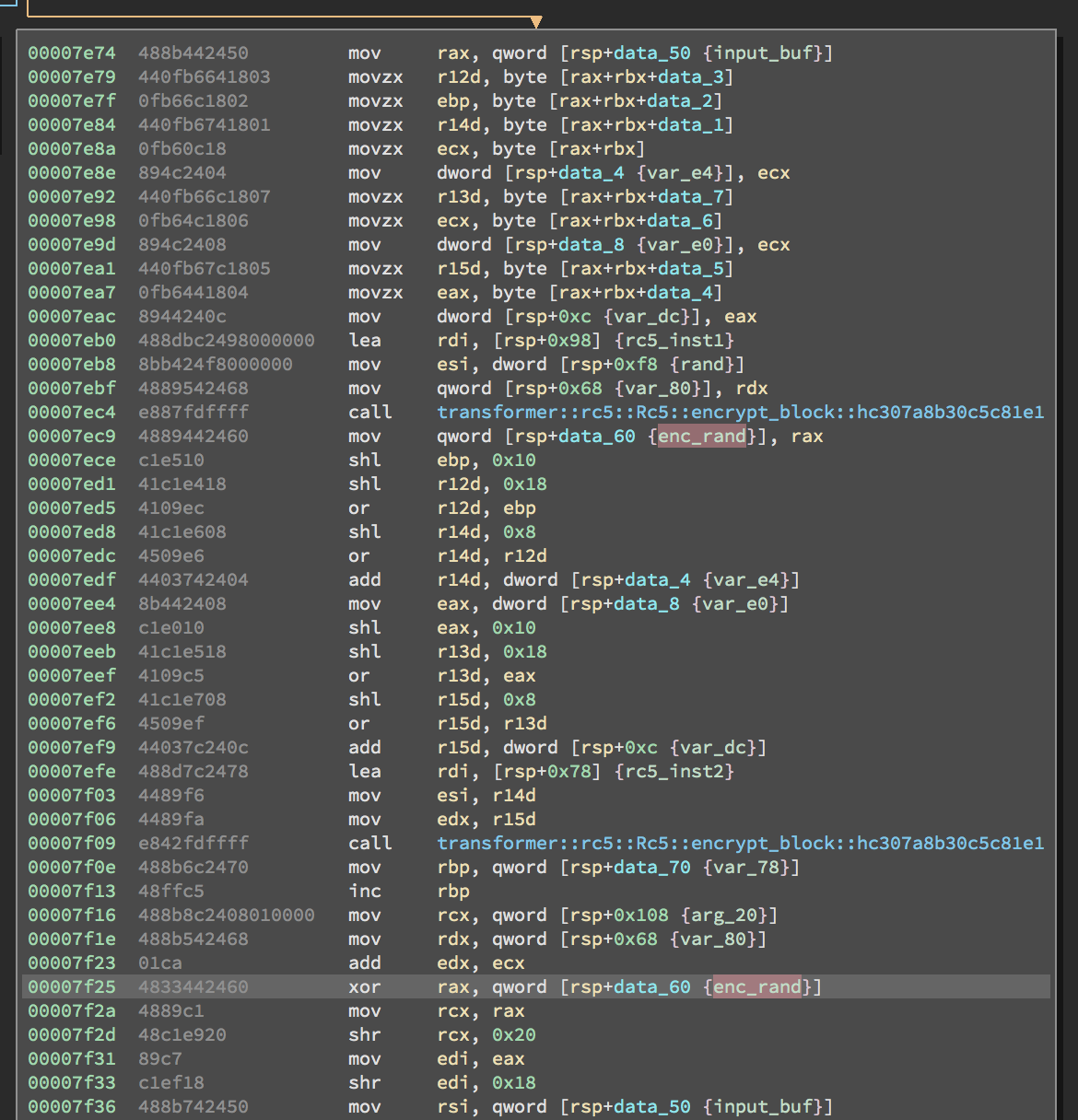
It appears as if the second RC5 instance is responsible for encrypting the input file, while the first RC5 instance encrypts something else altogether. Leaving whatever that is aside for now, we see that the output of each encryption is XORed together and stored into an output buffer.
What is the first instance operating on? Well, tracing the data flow is not
necessarily straightforward, but eventually we find that its input is a
combination of a random 32-bit value acquired from
rand::thread_rng().next_u32() and a 32-bit counter that starts at 0 and is
incremented by one for each 8-byte block that is processed by the program.
However, it’s not actually this simple. Some more analysis reveals that there are actually three threads concurrently processing separate “stripes” of the input file. That is to say, each thread processes blocks like below:
And, each thread processes a separate stripe of the input file:
The astute reader will immediately see that one stripe is not covered
whatsoever! So, we should see that stripe appear as plaintext in the
“encrypted” output of the tool. As we shall see, this will be confirmed when
actually running transformer.
Building a Decrypter
Since we have a pretty good idea of what’s going on with this challenge, it’s time to do some debugging to confirm our findings and build our decrypter. Let’s run the transformer on some known plaintext and see what we get.
Our input:
1"As democracy is perfected, the office of president represents, more and more
2closely, the inner soul of the people. On some great and glorious day the plain
3folks of the land will reach their heart's desire at last and the White House
4will be adorned by a downright moron."
5
6-- H.L. MenckenAnd, the output:
100000000 3e 0d 44 11 18 4c 02 09 63 f7 e8 29 ba bc 9b 4c |>.D..L..c..)...L|
200000010 87 2a ed c7 9a ea 98 3f b1 4a 43 a5 65 64 2c 20 |.*.....?.JC.ed, |
300000020 74 68 65 20 20 30 50 f3 2c 61 5f 66 65 0f 67 ea |the 0P.,a_fe.g.|
400000030 d3 4e c2 3a f3 19 c6 e1 6c 18 c7 10 65 73 65 6e |.N.:....l...esen|
500000040 74 73 2c 20 e4 62 3a 73 a3 81 98 52 cc 7a c2 86 |ts, .b:s...R.z..|
600000050 3d 07 8d 50 50 a1 fc 14 58 29 9f 27 68 65 20 69 |=..PP...X).'he i|
700000060 6e 6e 65 72 82 15 8b 18 bc f0 f7 7d 8f 57 30 8c |nner.......}.W0.|
800000070 0b a4 6a 8d 01 24 9e 89 0d f5 da 2a 20 73 6f 6d |..j..$.....* som|
900000080 65 20 67 72 12 44 8a 87 96 92 74 4b 09 1e 70 fa |e gr.D....tK..p.|
1000000090 87 1a de 8d e9 96 a2 e5 38 cb 8c 8a 20 70 6c 61 |........8... pla|
11000000a0 69 6e 0a 66 fd a3 4d f7 5a 96 d4 8a 43 5e 8f 95 |in.f..M.Z...C^..|
12000000b0 42 cf 7c b9 83 2f 48 59 8e 90 12 a9 61 63 68 20 |B.|../HY....ach |
13000000c0 74 68 65 69 0f 0e 7a 6c 6e 01 29 5d 01 bd 52 5f |thei..zln.)]..R_|
14000000d0 e6 8a cf 12 2f db fd 85 6d 31 c8 3a 20 61 6e 64 |..../...m1.: and|
15000000e0 20 74 68 65 47 fe 3e ec aa 9d 93 10 15 80 58 ed | theG.>.......X.|
16000000f0 63 44 3e 47 41 ea 92 a1 de b8 10 92 72 6e 65 64 |cD>GA.......rned|
1700000100 20 62 79 20 a0 fa da 10 a8 9a 50 5c 78 02 a7 c2 | by ......P\x...|
1800000110 5c 22 43 d5 5c 69 72 d1 a9 bc db 19 48 2e 4c 2e |\"C.\ir.....H.L.|
1900000120 20 4d 65 6e 94 a8 7d 36 41 0c e0 9e | Men..}6A...|
200000012cSo far, so good! We can immediately see that our hypothesis about the presence of plaintext in the output is confirmed. (If you’re unconvinced, take a look at bytes 0x1c-0x24, 0x3c-0x44, etc.)
Let’s take a closer look at the input and output.
1|"As democracy is| |>.D..L..c..)...L|
2| perfected, the | |.*.....?.JC.ed, |
3|office of presid| |the 0P.,a_fe.g.|
4|ent represents, | |.N.:....l...esen|
5|more and more.cl| |ts, .b:s...R.z..|
6|osely, the inner| |=..PP...X).'he i|
7| soul of the peo| |nner.......}.W0.|
8|ple. On some gr| |..j..$.....* som|
9|eat and glorious| |e gr.D....tK..p.|
10| day the plain.f| |........8... pla|
11|olks of the land| |in.f..M.Z...C^..|
12| will reach thei| |B.|../HY....ach |
13|r heart's desire| |thei..zln.)]..R_|
14| at last and the| |..../...m1.: and|
15| White House.wil| | theG.>.......X.|
16|l be adorned by | |cD>GA.......rned|
17|a downright moro| | by ......P\x...|
18|n."..-- H.L. Men| |\"C.\ir.....H.L.|
19|cken.| | | Men..}6A...| See anything suspicious? Well, it turns out that the plaintext is shifted four bytes in the ciphertext, which suggests that 4 bytes have been prepended to the output. Given that (if) the ciphertext is the result of an operation using a random value and that random value is 32 bits wide, you only get one guess for what the prepended value might be.
(Just to be clear: It’s the random value.)
Let’s try to confirm all of this. Using a homebrew scriptable debugger, we can introspect on the program at various points and dump relevant state.
This is a snippet of another trace where we can observe a couple of interesting facts.
1[...]
2Mar 27 16:56:30.970 DEBG keybuf1 = 5c3987caa89193a0
3Mar 27 16:56:30.973 DEBG keybuf2 = 7471956032af5f86
4Mar 27 16:56:30.976 DEBG plain_rand = rsi:11440d3e, rdx:00000000
5Mar 27 16:56:30.978 DEBG enc1 = 67e5bae2649e7834
6Mar 27 16:56:30.980 DEBG plain_text = "As demo
7Mar 27 16:56:30.982 DEBG enc2 = 1e1bb4d083a1b858
8Mar 27 16:56:30.984 DEBG xor = 79fe0e32e73fc06c
9Mar 27 16:56:30.986 DEBG enc_buf = 79fe0e32e73fc06c
10Mar 27 16:56:30.987 DEBG input_index = 32
11Mar 27 16:56:30.988 DEBG plain_rand = rsi:11440d3e, rdx:00000004
12Mar 27 16:56:30.990 DEBG enc1 = 2250a8ad9648395b
13Mar 27 16:56:30.992 DEBG plain_text = office o
14Mar 27 16:56:30.993 DEBG enc2 = d8f29e3223b0ab7c
15Mar 27 16:56:30.995 DEBG xor = faa2369fb5f89227
16Mar 27 16:56:30.997 DEBG input_index = 64
17[...]We see that our supposition about the static keys is correct (lines 2 and 3).
We also see that our 32-bit random value is indeed a constant that is
continually fed to the first RC5 instance (rsi, lines 4 and 11) along with a
block counter that is incremented on each iteration (rdx, lines 4 and 11).
(Note that the second block processed in the trace is thread 1’s second block,
so the input file offset 32 and block counter 4 also show how each thread is
responsible for its own file stripe.)
Finally, recall that we still haven’t narrowed down what the encryption mode is,
though we had a clue with the function name
transformer::mode::encrypt_crt_ecb. Well, things are now a lot clearer.
You’ll have to take my word for it, but the output of each RC5 instance is
deterministic regardless of block reordering, which accounts for the ECB
portion of the function name. And, I suppose that “crt” refers to the broken
counter mode implementation. Pretty clever!
With this knowledge in hand, writing a decrypter is a straightforward exercise (after finding a python implementation of RC5 in an old version of PyCrypto).
1#! /usr/bin/python2
2
3import sys
4import struct
5from Crypto.Cipher import RC5
6import IPython
7
8rounds = 16
9key1 = struct.pack('<Q', 0x5c3987caa89193a0)
10key2 = struct.pack('<Q', 0x7471956032af5f86)
11r1 = RC5.new(key1, word_size=32, mode=1, rounds=rounds)
12r2 = RC5.new(key2, word_size=32, mode=1, rounds=rounds)
13
14enc_data = open(sys.argv[1], 'rb').read()
15tmp_rand = enc_data[:4]
16dec_rand = ''
17for i in range(0, len(enc_data) / 4):
18 dec_rand += tmp_rand + struct.pack('<I', i)
19enc_data = enc_data[4:]
20enc_rand = r1.encrypt(dec_rand)
21
22tmp = []
23for i in range(len(enc_data)):
24 tmp.append(chr(ord(enc_data[i]) ^ ord(enc_rand[i])))
25xor_enc_data = ''.join(tmp)
26dec_data = r2.decrypt(xor_enc_data)
27
28result = ['\x00' for _ in range(len(dec_data))]
29for i in range(0, len(dec_data), 32):
30 result[i:i+24] = dec_data[i:i+24]
31 result[i+24:i+32] = enc_data[i+24:i+32]
32result = ''.join(result)
33
34open('soln.zip', 'wb').write(result)Let’s run the exploit.
1$ ./exploit.py ciphertext.zip.enc
2$ unzip -l soln.zip
3Archive: soln.zip
4 Length Date Time Name
5--------- ---------- ----- ----
6 1355 2017-03-06 11:58 plaintext.txt
7--------- -------
8 1355 1 fileConclusion
And with that, we have our flag:
This document defines four ciphers with enough detail to ensure interoperability between different implementations. The first cipher is the raw RC5 block cipher. The RC5 cipher takes a fixed size input block and produces a fixed sized output block using a transformation that depends on a key. The second cipher, RC5-CBC, is the Cipher Block Chaining (CBC) mode for RC5. It can process messages whose length is a multiple of the RC5 block size. The third cipher, RC5- CBC-Pad, handles plaintext of any length, though the ciphertext will be longer than the plaintext by at most the size of a single RC5 block. The RC5-CTS cipher is the Cipher Text Stealing mode of RC5, which handles plaintext of any length and the ciphertext length matches the plaintext length.
In the meantime your flag is VolgaCTF{Wh1te_b0x_crypto_i$_not_crYpto}.
The RC5 cipher was invented by Professor Ronald L. Rivest of the Massachusetts Institute of Technology in 1994. It is a very fast and simple algorithm that is parameterized by the block size, the number of rounds, and key length. These parameters can be adjusted to meet different goals for security, performance, and exportability.
RSA Data Security Incorporated has filed a patent application on the RC5 cipher and for trademark protection for RC5, RC5-CBC, RC5-CBC-Pad, RC5-CTS and assorted variations.